ときどき、YouTubeで、中学生や高校生の数学のサイト見たりします。この歳になり、受験という脅迫概念(?)の無い世界で、改めて、数学の授業を受けるとなかなか面白い事に気付いたりします。
水平線の距離について、余談で話されていました。地球は丸いので、有る一定の先まで見えてもその先は見えませんね。水平線までの距離は、三平方の定理で求める事ができるとのことでした。
三平方=3つの「平方」(2乗ということ)の定理、即ち X²+Y²=Z²ですね。
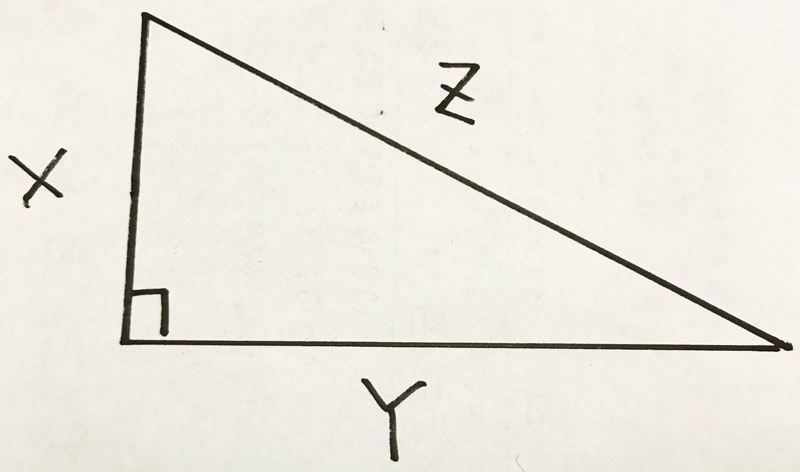
この定理で水平線わかるの?直角三角形って、どこにあるの?って思いますね。
有るんです。ずばり地球の中心-水平線ラインと 目線-水平線ラインが作る辺の交わりです。
地球は丸いので、水平線の地点で、90度の角度のところが、水平=見える限界です。
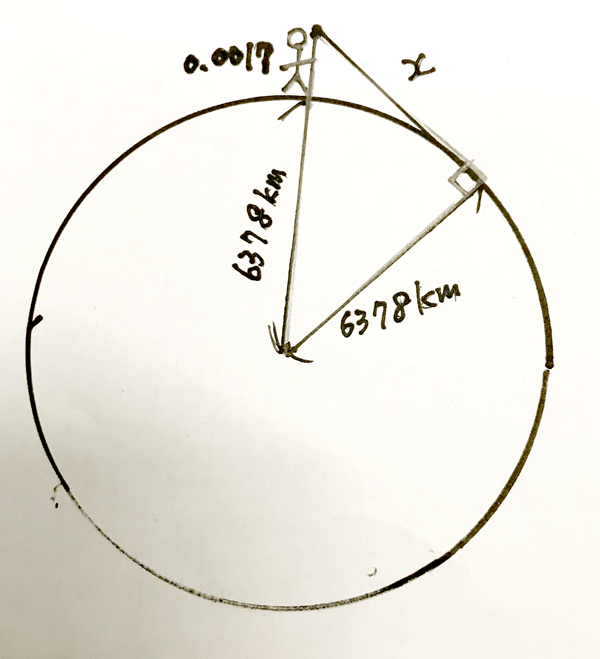
わかりやすく、身長何百キロメートルという超巨大な人間を想定するとこんな感じの絵ですね。
(実際は、斜辺と他の1辺が、ほぼ同じという、傍目には単なる直線に見える直角三角形となりますね)
 」
」
これを三平方の定理に当てはめると、地球の半径に人の目線の高さを足した長さが直角三角形の斜辺になりますので、
(地球の半径)²+(水平線X)²=(地球の半径+人の目線の高さ)²
身長180センチの人が、目線までの高さ170センチとして、
6378² +X² =(6378+0.0017)²
の方程式を解けば出てきます。
だいたい、水平線は、身長180センチくらいの人で、X=4.5キロほどだそうです。
もっとも、地球の半径といっても、地球は、楕円形らしくて(赤道付近の方が半径大きな数値)、場所により、地球の半径変わるので、正確な数値は実際は、もっとより高度な計算になるようですが…、
YouTubeの数学、面白いですね。
ps.事務員さんにこの話を説明すると、「水平線なんか図ることなんてないので、面白くもなんともなく、どうでもいい話です。そもそも地球の半径測った人がいるのですか?」と一蹴されました。



